Fungus is a prototype hardware specification of a Funge machine, a microcoded CPU capable of interpreting funges at the (macrocode) machine code level. Why? Well, so far we've had Lisp machines and Fortran machines and these days, right about everything is a C machine. I want a funge machine (the doctors tell me I harmless). This is based on an incomplete paper describing the architecture. It's perverted, it's baroque, it's vector-based, it's 18 bits wide and it was originally available in PDF. Here it is, in all its glory. If you think this is extreme, remember they were thinking about Java machines at one point.
January 2015
The page has been updated with more content in early 2015. There are samples of actual Assembly code for the project, and even a screenshot (the screenshot) of the old emulator running a simple ROM. Numerous errors have been corrected, including more typos than I care to admit.From the original HTML-ification in 2011
The original write-up is slightly incomplete, and has a number of errors (some more important than others). Some of these have been corrected in this version. Some haven't.1. Abstract
The Funge family of programming languages consists of a group of n-dimensional, stack-based programming languages. The most prominent and original member of the family, Befunge (a two-dimensional language), was invented in 1993 by Chris Pressey. The Funge family is Turing-Complete, yet was designed to be ‘a nightmare to compile’. Considering the author is aware of two compilers for Befunge, it would be reasonable to claim that Funge programmers are at home with nightmares. This paper describes Fungus, an architecture designed and optimised for Funge. It is hoped that this will give rise to further nightmares, possibly involving Cthulhu, dressed in an eldritch bikini of primordial horror, teaching INTERCAL to first-year law students.
Fungus is a microcoded, 18-bit, two-dimensional extreme RISC machine extremely suited to the interpretation of Funge at the hardware level. The author visualises the implementation of Funge compilers to generate Fungus-native code. The reader to whom the concept of Cthulhu in a bikini sounds acceptable may additionally visualise optimisingFunge compilers for Fungus.
2. Introduction
The Funge family of programming languages consists of a group of n-dimensional, stack-based programming languages. The most prominent and original member of the family, Befunge (a two-dimensional language), was invented in 1993 by Chris Pressey. Befunge, like its n-dimensional1 siblings, is Turing-complete, yet was designed to be ‘a nightmare to compile’. It can safely be said that Funges are ‘unusual’ languages. For an example, the following is the archetypal ‘Hello World’ programme in Unefunge (one-dimensional Funge):
052*"dlroW olleH">:#,_@
This programme already demonstrates quite a few of the features of a Funge (the syntax used here is the common denominator, Befunge '93): the existence of a stack; changing the direction of the PC; ‘0gnirts’-type strings et cetera. In the discussions to follow, it is assumed that the reader already knows at least Befunge '93. Otherwise, apart from boredom, insanity of click-happiness, the reader has little reason to be reading this page.
Compiling Funges is problematic because of their self-modifying tendencies and multi-directional PC. Befunge compilers are not impossible to write, but they are nightmarish, unless the programmer cheats subtly and ends up producing an interpreter. Considering there are at least two compilers for Befunge available, it would be reasonable to claim that Funge programmers are at home with nightmares.
Following the example of the (in)famous Lisp machines, would it not be possible to accelerate and facilitate the creation of a Funge system using dedicated hardware? Not only is this possible, it also an idea perverted enough to fit in with Funge itself.
This paper describes Fungus, an architecture designed and optimised for the execution of Funge software. It is hoped that this will give rise to further nightmares, quite likely involving Cthulhu in a bikini teaching INTERCAL to first-year law students.
Fungus is a microcoded, 16-bit, two-dimensional extreme RISC machine extremely suited to the interpretation of Funge at the hardware level. The author visualises the implementation of Funge compilers to generate Fungus-native code. The reader to whom the concept of Cthulhu in a bikini sounds acceptable may additionally visualise optimising Funge compilers for Fungus2.
The entire concept is theoretical, but a working emulator of Fungus can be built. Funge machines (like Lisp machines before them) can be utilised in the exploration of hack value, and as a means of punishing cocky undergraduates who think programming is an activity best done using a mouse. It is this author's belief that emerging programmers should be made painfully aware of the nightmares lurking in these Black Arts. The thorny path of Fear eventually leads to the green meadows of Knowledge. Or madness.
3. Design Aims
Certainly, any Turing-Complete architecture can run Funge, in the same was as any architecture can run Lisp. Fungus therefore aims to be a minimal microprocessor capable of supporting the execution of Funge at a low level. The following features are therefore desired:
Microcoded design. The processor is aware of a very small set of basic micro-instructions that help implement other, more complex macro-instructions. This allows Fungus to interpret various dialects of Funge.
Two-dimensional memory model. Since Befunge is by far the most common language of the family, this is also the dimensionality of the Fungus architecture. Befunge subsumes Unefunge, and higher dimensions could, potentially, be introduced to the architecture through hacking microcode. Memory is seen as two-dimensional, which is entirely acceptable, especially since certain types of DRAMs use a row/column scheme for address selection.
Vector registers. To support Funge at the lowest possible level, the architecture's PC is a ℤ2 vector (in Computer Science terms, a two-dimensional unsigned integer vector). An additional ΔPC register (also in ℤ2 is employed to provide the direction vector (in Physics terms, the velocity of the PC). For higher dimensionalities, the reader is urged to look at the works of Cray Research.
Hardware queue3. Although Funges are stack-based languages, recent dialects have introduced the ability to push values to either the bottom or top of the stack, and pull values from either the bottom or top of the stack. These preferences are user-selectable, leading to the so-called stack actually behaving more like two different queues or stacks. The author believes this to be an extremely perverse, counter-intuitive, bug-prone, paradigm-breaking design and applauds it wholeheartedly. Fungus embraces this ingenious bit of design and implements a hardware stack/queue using two stack pointer registers dealt with by microcode.
Hardware contexts4. In an effort to allow complex operating systems to run on Fungus (an additional form of punishment for rapidly despairing students), Funge implements hardware contexts, somewhat similar to and at the same time completely different from those of traditional memory managers. Hardware context registers allow delimiting a rectangular area of memory and allowing a program to run in it without having access to memory outside its own. The PC wraps around the edges of this region, thus forming a sub-torus of the super-torus that is Fungus' main memory. Lahey space is not supported by the hardware, but the masochistic topology enthusiast can still extract hours of pleasure attempting to visualise this sub-/super-torus relation.
Sharp blades. It is said UNIX gives one enough rope to shoot oneself in the foot. Fungus is required to conform to this time-honoured programming tradition, but the rope tricks are becoming dated. Hence, Fungus aims at providing one with enough sharp blades to shoot oneself in the foot. Various early-Eighties-style design flaws are introduced in an effort to make the user's life even more miserable.
Ease of implementation. Fungus is designed as a project that can be implemented using simple solid-state components (of the
74xxxfamily, for instance), or cheap FPGAs. This allows Funge to be inflicted on students taking Electrical Engineering, in addition to those taking Computer Science. It also increases hack value by allowing the reader to toy with the idea of physically building the processor, thereby making such a reader appear (to others) as a guru of esoteric hardware5.
4. Data Path
The design of Fungus intentionally resembles a simplified version of the MIPS R×000 architecture. The data path is built around a register file and an arithmetic/logic unit (ALU). Like the MIPS, most Fungus instructions involve the ALU and almost all involve the register file. Here is an explanation of the constituent parts, as outlined in the figure below:

Block diagram of the processor.
Register File (RF). A 8×18-bit RAM containing the values of the eight 18-bit registers of the CPU. The register file (RF) has two read (output) 18-bit ports A and B and one write (input) 18-bit port C. Each port can address independently any of the eight registers by means of three sets of three address lines each. An additional latch line clocks data from the input port into the register addressed by the C address lines.
Arithmetic/Logic Unit (ALU). This has two input ports (A and B) and one output port (C), all 18 bits wide. It also has three control lines to select the operation to be performed. The result of performing the selected operation on the two input ports appears on the output port after a certain stabilisation delay. An additional pair of control lines selects the current mask mode.
Memory Address Register (MAR). This 18-bit register can only be written by the CPU. It buffers and outputs an 18-bit address to the system's address bus. A control line latches data from the ALU's C (output) port into this register when this is required. The output of the MAR is tri-state, so that the address bus is only driven when needed, and left floating (in the high-impedance or Z state) at all other times.
Memory Register (MR). This register buffers and makes available data read from or written to system memory. This register has three ports. One is tri-state (bi-directional) and directly connected to the system's data bus; the other allows values from the ALU's C (output) port to be written to the register; and the third allows values to be read from the register.
Instruction Register (IR). This register is connected to the system's data bus and is latched during the fetch cycle. It contains the instruction word currently being executed. This is connected to the control unit and, indirectly, to the ALU.
A port multiplexer (A MUX). The A multiplexer selects one of two data sources for the ALU's port A. The two choices are the RF's A port (using a register's value as the left-hand operand); and the contents of the MR register (to access data read from memory). A single control line chooses among the two.
B port multipexer (B MUX). Like the A multiplexer, this unit selects among different data sources for the ALU's right-hand operand. There are three choices here: the value of the RF's B output port (to access a register's value); a value drawn from the current Instruction Register (IR), as processed by the Vector Control (VC) unit (to access literals embedded in the current instruction); or a value from the Constant Store (CS) ROM unit, to use a hardwired constant value. Two control lines choose among the three sources.
Vector Control (VC). This unit takes the literal 9-bit field the IR and either outputs it as a rd literal to the ALU, or copies the nine bits to both wo and rd and outputs the entire word to the ALU. This allows a 9-bit literal
Lto be used either as a scalar literal or as the vector(L,L). Combined with ALU masking modes, this unit can serve a number of functions. A single control line selects the behaviour of this unit.Constant Store (CS). This small 18-bit ROM contains a number of constants used in processing pico-code and other things. Scalars like 1, -1 and vectors
(1,1)and(-1,-1)are stored permanently in this ROM. Combined with masking modes in the ALU, this implements useful features and simplifies the CPU pico-code.Control Unit (CU). This unit is driven by the contents of the IR. It contains a ROM containing Very Long Instruction Word (VLIW) pico-instructions. Each bit of a pico-instruction directly drives one of the control signals controlling the various units of Fungus. A pico-PC steps through the ROM executing pico-instructions.
5. Programming Model
The Fungus programming model is both very familiar and very alien. It can certainly be described in terms of concepts very familiar to the average low-level programmer.
5.1. Word Length
Fungus is an 18-bit word machine. The author strongly believes in machines with word lengths that are not a multiple of four. The multiple-of-three approach is a time-honoured one, with support from such giants as IBM and Digital. Besides, forcing programmers to start thinking in octal after well nigh thirty years of thinking in hexadecimal works in accordance with Fungus philosophy6.
The system deals with 18-bit words and pairs of 9-bit wos and rds. These are known in mainstream computer science as most significant and least significant half-words, respectively.
An 18-bit quantity can have one of three interpretations, as illustrated in the figure below.

Fungus data types.
- An 18-bit scalar value, in the range 0–262,143.
- A ℤ2 vector, where the wo and rd represents the
yandxordinates respectively. The wo and rd are in the range 0–511. - The two ordinates of the vector representation may be accessed individually using instruction masking. This allows Fungus to access individual wos and rds in memory.
To the programmer, it is most convenient to write Fungus numbers in base eight (octal), with three octal digits to a wo or rd and six octal digits to a word.
5.2. Byte order
Fungus does not have bytes, hence no byte order. However, this specification doesrequire that the wo (y ordinate) is most significant. Hence, Fungus is wo-endian or y-endian.
5.3. Address Space
For convenience, the address space is identical to the word length: 18 bits wide. The programmer is free to use vectors or scalars to address memory, but Fungus convention uses vectors. Of the 18 address lines provided by the microprocessor, the most significant 9 (A9–A17) correspond to the wo and the y ordinate. The least significant 9 lines (A0–A8) correspond to the rd and the x ordinate. Thus, the maximum amount of memory addressable by Fungus is 256 kwords7.
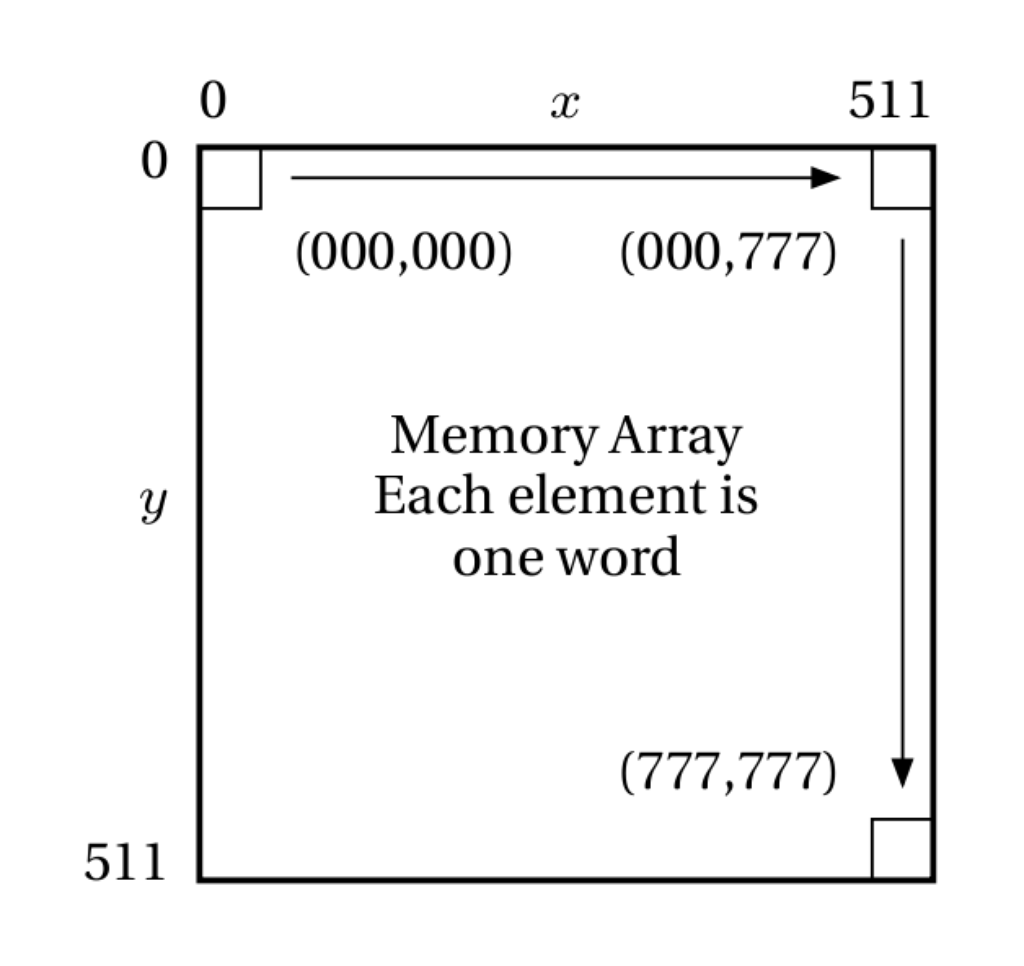
Fungus memory map.
Unlike conventional architectures, this memory is organised as a two-dimensional array, with 512×512 elements. Hence the use of vectors to address memory.
Interestingly, this vector view of memory is neither alien nor inconsistent with existing RAM technology. Most DRAM chips distinguish between ‘row’ and ‘column’ addresses and use external signals like CAS and RAS to change the semantics of their address pins. It would appear that computer technology has been building up to Fungus, doubtlessly the peak of CPU design for the discerning sadomasochist.
The topology of the address space is toroidal. This is a side effect of the use of vector registers. An intentional lack of overflow detection in the ALU allows wrapping around of vector ordinates to simulate this popular yet simple Funge topology.8
To further explain the topology, the programmer may address memory using vectors or scalars (though vectors are preferred). When addressing memory as a one-dimensional array by using scalar arithmetic, address 001777 + 1 yields address 002000. This is congruent with memory on conventional architectures. In vector mode, address 001777 + 1is equivalent to (001, 777) + (000, 001): this wraps around the X axis to (001, 000)or 001000. This is congruent with the toroidal topology and the way Funges generally work.
5.4. Memory
Memory also consists of 18-bit words. Fungus only reads and writes 18-bit quantities. Thus, the 256 kwords of accessible memory is 18-bits wide.
For the byte-o-philiac reader, a Fungus word is 2.25 bytes. A single 512-word row or column of memory is 1,152 bytes (1.125 kbytes). The entire address space corresponds to 589,824 bytes, or 576 kbytes. This, however, is irrelevant: values cannot be accessed in byte-sized chunks but only in word-sized quanta.
The address space may be expanded using memory mapping, swapping and paging techniques with external, kludgy hardware. Again, this is consistent with Fungus design.
5.5. Registers
As seen in the figure below, Fungus has eight word-wide registers. Registers may be treated as 18-bit scalar values and two-dimensional vectors with 9-bit wo and rd ordinates. The registers are referred to by number as $0–$7 (pronounced ‘big-money-zero’), or by name. All registers can be used as general purpose registers by the programmer who points loaded guns at her feet, but in reality, all but three registers have special uses:
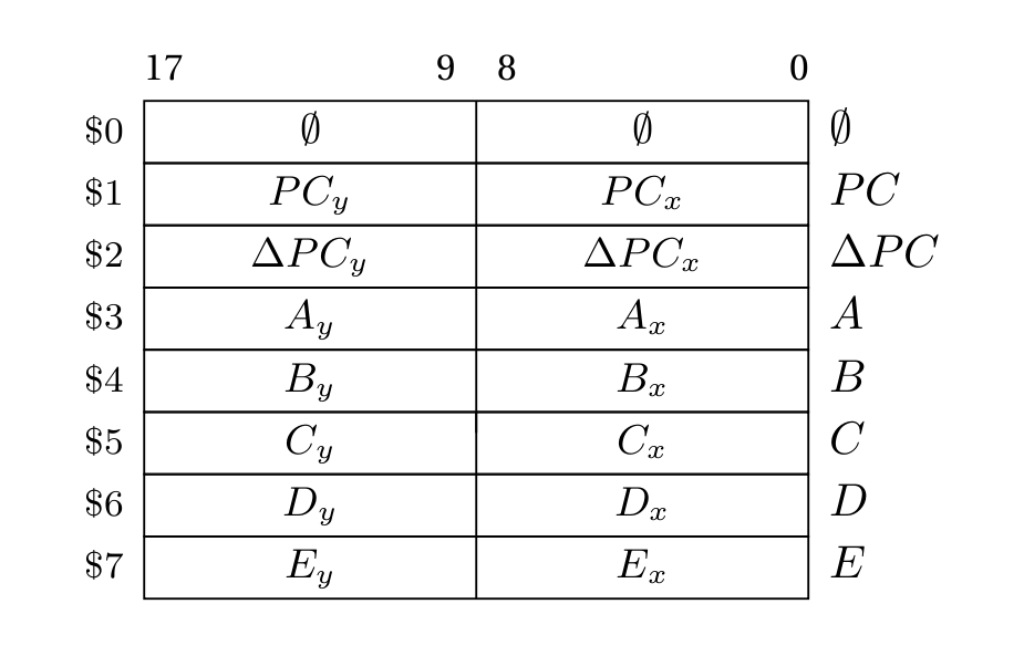
The Fungus register file.
$0or0: a source of zeroes. In compliance with Fungus design philosophy, this register is writable. Changing it, however, will massively disrupt CPU operation as$0is used internally by CPU picocode. There is purposefully no guard against this. Low level programming should be a disciplined discipline.$1orPC: the program counter. Like all other CPUs, this register points to the next instruction to be fetched from memory. Unlike all other CPUs, thePCis a vector.$2orΔPC: the program counter delta (velocity). This vector value is added to thePCvector immediately after an instruction fetch. The ordinate values are arbitrary, though values of -1 (left or up), 0 (no change) and 1 (right, down) are typical. Here are a few examples of usefulΔPCvalues:(000,000): halts the CPU (PC stops moving).(777,000): PC moves to the north.(001,000): PC moves to the south.(000,777): PC moves to the east.(000,001): PC moves to the west.- Diagonal movement is, of course possible, as are flying PCs, though these should not be attempted by the faint of heart. Lahey space is not available, the only available topology is the traditional torroidal one.
$3orA: the first general purpose register.$4orB: the second general purpose register.$5orC: the third and last general purpose register.$6orD: A general purpose register. This one is used to store temporary copies of theΔPCregister by theTRPcommand. It can still be used outside system traps/micro-instructions.$7orE: likewise, this register may hold temporary copies of thePCregister during aTRP.
6. CPU Architecture
Many CPUs of the past have been microcoded. Machine code instructions are internally interpreted as short programmes in microcode. Fungus takes a few extra steps towards the Cliffs of Insanity by introducing pico-instructions and pico-code. The CPU is built on top of a simple9Very Long Instruction Word (VLIW) core, as a multi-layer architecture.
Pico-code. Executed inside the CPU, Fungus pico-code is a simple VLIW machine language. Pico-code is immutable and resides in a ROM inside the CPU. It translates instructions to control signals for the CPU's component units. Pico-code is not accessible by the programmer.
Microcode. Is the lowest possible level of machine code executed by the CPU. This is a RISC machine language, with one instruction per word. Microcode is not mutable in itself, but it is expandable using user defined traps.
Befunge code. This can be implemented as a set of traps in microcode. Each Befunge instruction is the least significant 8 bits of an instruction word, the remaining 10 bits being zero. The instructions are interpreted and executed in Microcode. Other versions of Befunge can be implemented by redefining the traps; a feature that allows for diverse lower extremity injuries via chemically propelled metal projectiles.
7. Instruction Set
Fungus is a Reduced Instruction Set Computer (RISC). The instruction set is as small as possible. There are 26 instructions and they are all one word wide. Instructions are not executed in a single clock tick. They range from three to eight cycles10, with most instructions needing three.
7.1. Addressing Modes
Fungus does not have the usual large family of addressing modes. In fact, the mention of addressing modes with respect to this architecture is officially deprecated. However, in the interest of providing an explanation to users hopelessly lodged in this paradigm, here is a list of ‘addressing modes’:
Immediate. An instruction operates on a literal, storing the address in a register.
Indexed. An instruction accesses memory by applying an arithmetic or logic operation on two register values, and using the result as the memory address. The result of the instruction is stored in the target register.
Register. An instruction operates on one or two registers, storing the result in a third, target register.
7.2. Masking Modes
Since Fungus is a ℤ2 machine, it needs to deal with vector values, but also with their ordinates in an independent fashion. To provide necessary facilities, it also needs to access words as scalar values. This duplication of functionality would increase unacceptably the size of the instruction set. Thus, in the interest of additional obfuscation, masking modes were introduced. Not to be mistaken with addressing modes, masking modes modify the semantics of instructions as follows:
Vector mode. This is the default. The wo and rd parts of a word are treated independently. Literals are written like
(123,456)(although this is not necessary; the same literal could still be written123456). The result of777000 + 001001would be000001. In vector notation:(777, 0) + (1, 1) = (0, 1).X mode. This mode masks the wo (y ordinate) part of words. In this way, all instructions affect only the rd (x ordinate) part of data. In this context, the addition
(777, 0) + (1, 1)yields(777, 1).Y mode. As above, but the rd (x ordinate) part of data is masked, making it immutable.
Scalar mode. Treats words as scalars. In scalar mode, the addition
115333 + 225511would yield343044(note how the carry crosses the wo-rd boundary).
7.3. Instruction Format
There are two groups of instructions: group 0 involves a target register and 9-bit literal; group 1 involves a target register and one or two source registers. The two groups are illustrated in the figure below:
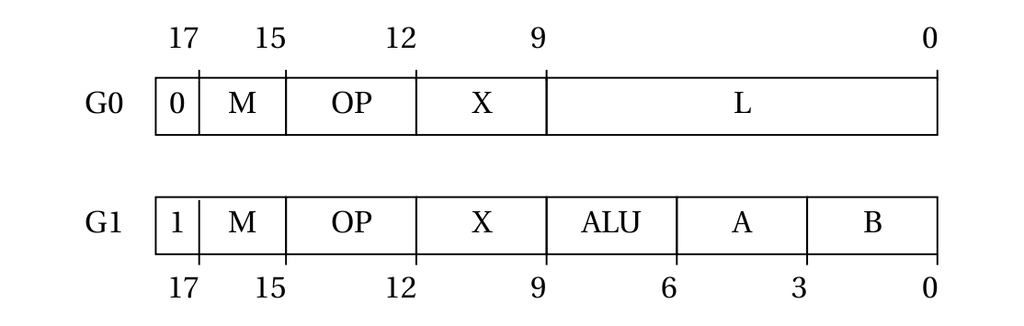
Fungus instruction format.
The formats themselves are as follows:
Group 0. Comprises of the following fields (in order of increasing significance):
L: 9 bits. A 9-bit literal argument.X: 3 bits. The target register.OP: 3 bits. The instruction opcode.M: 2 bits. Masking mode.0: 1 bit. The instruction group (always 0).
Group 1. Comprises of the following fields (in order of increasing significance):
B: 3 bits. For binary instructions, the register used as right-hand operand. For unary instructions, this field acts as an extension of the ALU field.A: 3 bits. The register used as left-hand operand.ALU: 3 bits. The ALU op code.X: 3 bits. The target register.OP: 3 bits. The instruction opcode.M: 2 bits. Masking mode.1: 1 bit. The instruction group (always 1).
Masking modes (the M instruction field) are as follows:
00is the scalar mode, denoted in Assembly by the.ssuffix.01is the rd (X) mode. Assembly suffix:.x.10is the wo (Y) mode. Assembly suffix:.y.11is the default, vector mode. Assembly suffix:.v(or none, as it is the default)
The complete Fungus instruction set is shown in the following two tables.
| Group 0 Instructions | ||||
|---|---|---|---|---|
| G | Op | Cycles | Instruction | Semantics |
| 0 | 000 | 8 | TRP L | TPC ← PC; TΔPC ← ΔPC; PC ← (L,0); ΔPC ← (-1,0) |
| 0 | 001 | 4 | LI X,L | X ← L |
| 0 | 010 | 4 | LV X,L | X ← (L,L) |
| 0 | 011 | 5/6 | SZ X,L | X = 0 ⇒ PC ← PC + ΔPC |
| 0 | 100 | 5/6 | SNZ X,L | X ≠ 0 ⇒ PC ← PC + ΔPC |
| 0 | 101 | 7/8 | DZ X,L | ΔPC ← (-1,-1); X = 0 ⇒ ΔPC ← (1,1) |
| 0 | 110 | 7/8 | DNZ X,L | ΔPC ← (-1,-1); X ≠ 0 ⇒ ΔPC ← (1,1) |
| 0 | 111 | 5 | RET | PC ← TPC; ΔPC ← TΔPC |
| Group 1 Instructions | ||||||
|---|---|---|---|---|---|---|
| G | Op | ALU | B | Cycles | Instruction | Semantics |
| 1 | 000 | 000 | B reg | 4 | ADD X,A,B | X ← A + B |
| 1 | 000 | 001 | B reg | 4 | SUB X,A,B | X ← A - B |
| 1 | 000 | 010 | B reg | 4 | AND X,A,B | X ← A ∧ B |
| 1 | 000 | 011 | B reg | 4 | OR X,A,B | X ← A ∨ B |
| 1 | 000 | 100 | B reg | 4 | XOR X,A,B | X ← A ⊗ B |
| 1 | 000 | 111 | 000 | 4 | NOT X,A | X ← ¬A |
| 1 | 000 | 111 | 001 | 4 | SHR X,A | X ← ⌊A/2⌋ |
| 1 | 000 | 111 | 010 | 4 | INV X,A | X ← X + (1,1) |
| 1 | 000 | 111 | 011 | 4 | DEV X,A | X ← X - (1,1) |
| 1 | 001 | ∘ | B reg | 5 | LW X,A∘B | X ← [A ∘ B] |
| 1 | 010 | ∘ | B reg | 5 | LX X,A∘B | Xx ← [A ∘ B]x |
| 1 | 011 | ∘ | B reg | 5 | LY X,A∘B | Xy ← [A ∘ B]y |
| 1 | 100 | ∘ | B reg | 5 | SW X,A∘B | [A ∘ B] ← X |
| 1 | 101 | ∘ | B reg | 5 | SX X,A∘B | [A ∘ B]x ← Xx |
| 1 | 110 | ∘ | B reg | 5 | SY X,A∘B | [A ∘ B]y ← Xy |
Underlined operations are subject to the current masking mode. For simple operations like ALU operations, the masking mode applies to the the entire instruction.
8. Instruction Reference
This section describes in detail the Fungus instruction set. The instruction set is broken into arithmetic/logic binary operations, arithmetic/logic unary operations, literals, memory input/output, flow control, and some brief examples of proposed macro-instructions.
8.1. Arithmetic and Logic Binary Operations
All instructions in this category are G1 instructions. In fact, they are the same instruction: ALU, engaging the ALU in different operation modes. For the programmer's convenience, the ALUinstruction is assembled and disassembled as different sub-instructions, depending on the contents of the ALU instruction field. Since binary arithmetic and logic instructions are effectively one instruction, semantics are the same throughout. Only the arithmetic or logic operation differs.
8.1.1. Operation
These instructions apply an arithmetic or logic operation on the contents of registers A (denoted by bits aaa) and B (denoted by bits bbb) and store the result in register X (denoted by bits xxx).
8.1.2. Masking Modes
Use of Masking Modes modifies the way arithmetic/logic is performed and masks the result. Vector mode (e.g. ADD.v or simply ADD) adds vector operands (wo and rd ordinates added separately). Scalar mode (e.g. XOR.s) treats register contents as 18-bit words. X and Y modes (e.g. SUB.x and AND.y respectively) add only the rd and wo parts of a word respectively, leaving the rest untouched.
8.1.3. Examples
The easiest and most illustrative instruction is, of course, addition. Using initial register values $1=123456, $2=654321, $3=555555, $4=$5=$6=$7=222222, the following instructions can be executed:
ADD $4,$1,$2 ; $4 is now 777777
ADD.x $5,$1,$2 ; $5 is now 222777
ADD $6,$1,$3 ; $6 is now 700233
ADD.s $7,$1,$3 ; $7 is now 701233
Final register values: $4=777777, $5=222777, $6=700233, $7=701233. Note the difference between the last two instructions. The Scalar mode instruction (.s prefix) propagates the carry past the wo/rd boundary, whereas the default, vector mode does not.
8.1.4. ADD — Add registers
| Instruction | ADD x,a,b |
|---|---|
| Format | 1mm 000 xxx 000 aaa bbb |
| Semantics | X ← A + B |
| Cycles | 4 |
8.1.5. SUB — Subtract registers
| Instruction | SUB x,a,b |
|---|---|
| Format | 1mm 000 xxx 001 aaa bbb |
| Semantics | X ← A - B |
| Cycles | 4 |
8.1.6. AND — Bitwise And
| Instruction | AND x,a,b |
|---|---|
| Format | 1mm 000 xxx 010 aaa bbb |
| Semantics | X ← A ∧ B |
| Cycles | 4 |
Since there is no carry, this instruction works in exactly the same way in both Vector and Scalar modes.
8.1.7. OR — Bitwise Or
| Instruction | OR x,a,b |
|---|---|
| Format | 1mm 000 xxx 011 aaa bbb |
| Semantics | X ← A ∨ B |
| Cycles | 4 |
Since there is no carry, this instruction works in exactly the same way in both Vector and Scalar modes.
8.1.8. XOR — Bitwise Exclusive Or
| Instruction | XOR x,a,b |
|---|---|
| Format | 1mm 000 xxx 100 aaa bbb |
| Semantics | X ← A ⊗ B |
| Cycles | 4 |
Since there is no carry, this instruction works in exactly the same way in both Vector and Scalar modes.
8.2. Arithmetic and Logic Unary Operations
Instructions in this category are cascaded extensions of the ALUinstruction, where the ALU operation is 111 and the Binstruction field selects a unary ALU operation instead of a register. These are, of course, G1 instructions.
8.2.1. Operation
These instructions apply an arithmetic or logic operation on the contents of register A (denoted by bits aaa), storing the result in register X (denoted by bits xxx).
8.2.2. Masking Modes
As always, use of masking modes modifies the way arithmetic/logic is performed and masks the result. Vector mode (e.g. DEV) increases vector operands (wo and rd ordinates increased separately). Because of the logic or kludgy nature of most of these instructions, masking modes do not work as expected. Please read along for more details following each instruction.
8.2.3. NOT — Bitwise Negation
| Instruction | NOT x,a,b |
|---|---|
| Format | 1mm 000 xxx 111 aaa 000 |
| Semantics | X ← ¬A |
| Cycles | 4 |
Masking Modes: since there is no carry, this instruction works in exactly the same way in both Vector and Scalar modes. In X and Y modes, only the rd and wo of the target register are modified respectively.
8.2.4. SHR — Shift Right
| Instruction | SHR x,a |
|---|---|
| Format | 1mm 000 xxx 111 aaa 001 |
| Semantics | X ← ⌊A/2⌋ |
| Cycles | 4 |
This instruction halves the source register, rounding down. The most significant bit (or bits, in vector mode — see below) are zero-padded. There is no corresponding SHL instruction. This can be simulated at the assembly level using the ADD instruction. Hence SHL
x,a is equivalent to ADD x,a,a (a left shift effectively doubles the operand). In the interest of simplicity, only single bit shifts are available.
Masking Modes: in Vector mode, the wo and rd parts of a word are shifted separately. In scalar mode, the entire word is shifted in unison. In X and Y modes, the rd and wo are respectively shifted without disturbing the other half of the target register.
Examples
Using $1=123456 and $4=$5=$6=$7=333333:
SHR.s $4,$1 ; $4 is now 051627
SHR.x $5,$1 ; $5 is now 333227
SHR.y $6,$1 ; $6 is now 051333
SHR $7,$1 ; $7 is now 051227
Note the difference between the scalar and vector instructions. Shifted bit values do not cross the wo/rd boundary in vector mode. Also of note is the third instruction which shifts 123 (83 in base 10) to the right yielding 51 (41 in base 10), rounding down.
8.2.5. INV — Increment Vector
| Instruction | INV x,a |
|---|---|
| Format | 1mm 000 xxx 111 aaa 010 |
| Semantics | X ← A + (1, 1) |
| Cycles | 4 |
This unusual instruction is useful in incrementing vector pointers. It increments a vector by adding (1, 1) to it. At first it sounds inane, but masking modes turn this instruction to a powerful tool. Grasping the use of INV (and a few other similar instructions) is an important part of understanding fully the mentality of the Fungus architecture.
Masking modes: in Vector mode, the vector value of register a is incremented along the main diagonal by adding the vector (1, 1) to it. In X mode, only the rd is incremented, effectively moving the vector register a along the X axis. In Y mode, only the wo is incremented, effectively moving the vector register a along the Y axis. In scalar mode, the constant 001001 is added to register a. In vector terms, the register moves along the main diagonal (in computer, up-is-negative terms).
Examples
Using $1=$6=$7=123456:
INV $5,$1 ; $7 is now 124457
INV.x $6,$1 ; $5 is now 123457
INV.y $7,$1 ; $6 is now 124456
8.2.6. DEV — Decrement Vector
| Instruction | DEV x,a |
|---|---|
| Format | 1mm 000 xxx 111 aaa 011 |
| Semantics | X ← A - (1, 1) |
| Cycles | 4 |
Works like INV, but decrements vectors.
Masking modes: works like INV, but the constant vector (1, 1) (or the scalar 001001) is subtracted from register a and stored in register x.
8.2.7. INC — Increment Scalar
| Instruction | INC x,a |
|---|---|
| Format | 1mm 000 xxx 111 aaa 100 |
| Semantics | X ← A + 1 |
| Cycles | 4 |
This mundane, scalar counterpart of INV increments a scalar value. This is a particularly kludgy instruction, but needed for many uni-dimensional tasks. As such, it lacks the elegance of most other Funge instructions11.
Masking modes:
In Vector mode, the vector (0, 1) is added to register a. In X mode, this instruction behaves exactly like INV.x. In Y mode, this is a NOP. In scalar mode, register x receives the scalar value a + 0000001.
Examples
Using $1=123456, $4=$5=$6=$7=000000:
INC $4,$1 ; $7 is now 123457
INC.s $5,$1 ; $7 is now 123457
INC.x $6,$1 ; $5 is now 123457
INC.y $7,$1 ; $6 is now 123456
8.2.8. DEC — Decrement Scalar
| Instruction | DEC x,a |
|---|---|
| Format | 1mm 000 xxx 111 aaa 101 |
| Semantics | X ← A - (0,1) |
| Cycles | 4 |
DEC12 works like INC, but decrements scalars.
Masking Modes: works like INC, but the constant (0,1) (or the scalar 000001) is subtracted from register a and stored in register x.
8.3. Literals
Loading registers with literal values is needed by any self respecting architecture. Like the MIPS R×000, Fungus has a fixed single-word instruction length, which precludes loading an entire literal word into a register. A pair of instructions are therefore provided, but, in true Fungus fashion, they are not what the MIPS programmer would expect.
8.3.1. LI — Load Literal
| Instruction | LI x,L |
|---|---|
| Format | 0mm 001 xxx LLLLLLLLL |
| Semantics | X ← L |
| Cycles | 4 |
This instruction loads a literal value into a register's rd. Since the literal L is only 9 bits wide, only the rd can be affected. The wo is zero-padded. To set a wo to a literal value, please use LV.y.
Masking Modes: in Vector and Scalar modes, LI and LI.s simply copy the zero-padded literal L to register X. In X mode, the literal overwrites the rd of register X. The wo is not modified. In Y mode, this instruction zeroes the wo of the target register without modifying the rd.
Examples
Here are a few examples of the use of LI, where $6=$7=555555:
LI $4,145 ; $4 is now 000145
LI.s $5,145 ; $7 is now 000145
LI.x $6,777 ; $5 is now 555777
LI.y $7,666 ; $6 is now 000555
Note how Scalar and Vector modes work in an identical fashion. Also noteworthy is the unusual LI.y construct that zeroes an rd.
8.3.2. LV — Load Vector
| Instruction | LV x,L |
|---|---|
| Format | 0mm 010 xxx LLLLLLLLL |
| Semantics | X ← (L, L) |
| Cycles | 4 |
Yet another unusual instruction. This one duplicates L to form the vector \((L,L)\), which it then stores in register X.
Masking modes: in Vector and Scalar modes, LVand LV.s simply copy the literal vector (L,L) or the scalar (29 + 1)L = 513L (of doubtful usefulness unless base 513 math is attempted) to the target register. In X mode, this instruction behaves exactly like an LI.x. In Y mode, the most useful invocation, L is stored in the wo of the target register.
Examples
Here are a few examples of the use of LV, where $6=$7=555555:
LV $4,145 ; $4 is now 145145
LV.s $5,707 ; $5 is now 707707
LV.x $6,777 ; $6 is now 555777
LV.y $7,666 ; $7 is now 666555
Note how Scalar and Vector modes work in an identical fashion and the use of LV.y to load a literal into a wo.
8.4. Input/Output
Memory input and output is accomplished through the abuse of six G1 instructions (dealing with indexed register memory access). The G1 instructions incorporate and subsume the ALU instruction. As such they could be seen as 66 different instructions, but this author will not because it's not convenient enough13.
Operation. These instructions apply an arbitrary arithmetic or logic binary or unary operation on the contents of registers A (denoted by bits aaa) and B (denoted by bits bbb, naturally only used on binary operations). Masking modes apply to the the result of the operation as usual.
The result is then used to address memory. Load instructions transfer a word, wo or rd from that location in memory to the X register. Store instructions transfer a word from register X to the resultant location in memory. This last case is the only exception in the use of register X as a target register: Store instructions use memory as a target and register X as a source.
Obviously, not all arithmetic and logic operations will be useful in addressing memory. However, the elegance14 of Fungus is such that using obscure operations is not forbidden. It is, in fact, encouraged.
In the instruction descriptions below, the symbol ∘15 denotes an arithmetic or logic operation, either binary or unary. Where the operation is unary, the nazg is written in prefix fashion. The following table lists ALU operations and their nazg symbols.
| Op | ALU | B | Nazg Expression (C-like) |
|---|---|---|---|
ADD | 000 | B | a + b |
SUB | 001 | B | a - b |
AND | 010 | B | a ∧ b (a & b) |
OR | 011 | B | a ∨ b (a | b) |
XOR | 100 | B | a ⊗ b (a ^ b) |
NOT | 111 | 000 | ¬a (~a) |
SHR | 111 | 001 | ⌊a/2⌋ (a >> 1) |
INV | 111 | 010 | a + (1,1) (a + 01001) |
DEV | 111 | 011 | a - (1,1) (a - 01001) |
INC | 111 | 100 | a + 1 |
DEC | 111 | 101 | a - 1 |
Masking modes: in the context of load and store instructions, masking modes work slightly less intuitively than expected. Masking is only applied to the memory address calculation, not the entire operation. All of LW, LW.x, LW.yand LW.s load entire words from memory. The difference is in the way the memory addresses are calculated.
In vector mode, registers A and B are treated as vector values, and behave as specified in the corresponding ALU operation. In scalar mode, registers A and B behave like scalars, with carry crossing the wo/rd boundary, et cetera. Modes X and Y are not particularly useful. They respectively apply the operation on the rd and wo, but the other half of the word is filled with zeroes.
Examples
Here are a few examples of the flexibility afforded by this scheme, where $4=123456, $5=111111and $6=555555:
LW $4,$5+$6 ; $4 is mem[666666]
LW $4,$5|$6 ; $4 is mem[555555]
LX $4,$5^$6 ; $4.x is mem[444444].x
LW.x $4,$5+$6 ; $4 is mem[000666]
SY.x $4,$5&$6 ; mem[000111].y is (123456).y
SW $4,+$5 ; mem[111112] is 123456
Note how the .x mode in the fifth example applies the address calculation to the rd only, but, since SY is used, a wois written to memory,
8.4.1. LW — Load Word
| Instruction | LW x, a ∘ b** or **SW x, ∘b |
|---|---|
| Format | 1mm 001 xxx alu aaa bbb |
| Semantics | X ← [A ∘ B] |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result to retrieve a whole word. The word is stored in register X.
8.4.2. LX — Load Rd
| Instruction | LX x, a ∘ b** or **SX x, ∘b |
|---|---|
| Format | 1mm 010 xxx alu aaa bbb |
| Semantics | rd(X) ← rd([A ∘ B]) |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result to retrieve an rd only. The rd is stored in register X's rd.
8.4.3. LY — Load Wo
| Instruction | LY x, a ∘ b** or **SY x, ∘b |
|---|---|
| Format | 1mm 011 xxx alu aaa bbb |
| Semantics | wo(X) ← wo([A ∘ B]) |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result to retrieve a wo only. The wo is stored in register X's wo.
8.4.4. SW — Store Word
| Instruction | SW x, a ∘ b** or **SW x, ∘b |
|---|---|
| Format | 1mm 100 xxx alu aaa bbb |
| Semantics | [A ∘ B] ← X |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result. The word contained in register X is stored at that address.
8.4.5. SX — Store Rd
| Instruction | SX x, a ∘ b** or **SX x, ∘b |
|---|---|
| Format | 1mm 101 xxx alu aaa bbb |
| Semantics | rd([A ∘ B]) ← rd(X) |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result. The rd contained in register X is stored at that address' rd.
8.4.6. SY — Store Wo
| Instruction | SY x, a ∘ b** or **SY x, ∘b |
|---|---|
| Format | 1mm 110 xxx alu aaa bbb |
| Semantics | wo([A ∘ B]) ← wo(X) |
| Cycles | 5 |
Evaluates A nazg B (or nazg A for unary operations) and addresses memory with the operation result. The wo contained in register X is stored at that address' wo.
8.5. Flow Control
Flow control is implemented by means of three pairs of instructions.
- The trap mechanism includes
TRPandRETis a cross between the subroutine calling of most architectures, x86 software interrupts and Motorola 68k traps. Traps can be used to build up to 512 macro-instructions or system services, or to implement Befunge on top of Fungus. - The skip mechanism includes the
SZandSNZinstructions. These skip the next instruction depending on the value of the specified register. - The divert mechanism includes the
DZandDNZinstructions. These modify (divert) theΔPCregister and hence the direction of the PC based on the value of the specified register.
8.5.1. TRP — Trap
| Instruction | TRP L |
|---|---|
| Format | 0XX 000 XXX LLLLLLLLL |
| Semantics | TPC ← PC; TΔPC ← ΔPC; PC← (L, 0); ΔPC←(-1, 0) |
| Cycles | 8 |
Bits marked ‘X’ in the instruction format above are Don't-Care values. The target register field is ignored and assembly notation of TRP omits it altogether.
This is the most complex Fungus instruction. It works as follows: the PC and ΔPC registers are saved in the TPC ($7) and TΔPC ($6) registers respectively; then ΔPC is made to point ‘north’ and PC is assigned the vector (0, L). This effectively jumps to a specified subroutine on the first row of memory, with the PC pointing north. The subroutine performs any processing necessary and issues the RET instruction to return to the caller.
These traps can be used for interrupt handling, system service vectors, and to implement Befunge as a set of macro-instructions built on top of Fungus.
The observant reader will no doubt have noticed that the instruction format for TRP uses don't-care values for the ALU and MM fields. By convention, the wo of a trap instruction is typically 0 and the rd denotes the trap to jump to. That makes the instruction have a bitmap of 000000000
LLLLLLLLL.
Traps 040–177 (i.e. decimal 32–127) correspond to the 96 printable ASCII characters (padded with 11 zero bits). These can be issued on most modern keyboards.
In this way, plain text files comprising printable ASCII characters are seen as sequences of trap instructions by Fungus, which encode a program in what is actually a concatenative language16. Each trap performs one Funge instruction and returns to the caller. In this manner, complex Funges can be implemented cleanly and elegantly on top of the lower-level Fungus instruction set. At the same time, Fungus machine code can still be mixed in with high-level Befunge instructions for added hack value.17
Trap vectors are arranged on the row 0 of the address space for two reasons:
- RAM is expected to be mapped onto the address space starting with row 0.
- Fungus boot ROM can modify row 0 to displace the PC either ‘north’ or ‘south’. If the PC points north, a trap will cause the PC to wrap around to row 777, where ROM is expected to be mapped. Thus the default ROM handler for a trap may be set. Making the PC point south allows user-supplied traps to be implemented, since the next instruction to be executed will be on row 1 of RAM.
Masking modes: masking modes do not apply to the TRP command and are ignored. Convention dictates mode 00 is used, i.e. scalar mode.
Example
The Unifunge programme 52*. that evaluates and prints out ‘10’ looks as follows in 18-bit octal words: 000065 000062 000052
000056. This disassembles into the following Fungus code, for a hypothetical Befunge programming environment.
TRP 065 ; '5': Push 5
TRP 062 ; '2': Push 2
TRP 052 ; '*': Multiply
TRP 056 ; '.': Print number
8.5.2. RET — Return
| Instruction | RET |
|---|---|
| Format | 0XX 001 XXX XXXXXXXXX |
| Semantics | PC ← TPC; ΔPC ← TΔPC |
| Cycles | 5 |
Bits marked ‘X’ in the instruction format above are don't-care values. Both target register and literal value are ignored for this instruction. No arguments need to be passed to it in assembly.
This instruction marks the end of a trap handler. It simply restores the values of the PC and ΔPC registers using the values stored by the TRP instruction.
Masking modes: these do not apply to the RETcommand and are ignored.
8.5.3. SZ — Skip If Zero
| Instruction | SZ A |
|---|---|
| Format | 0mm 011 XXX XXX aaa XXX |
| Semantics | X = 0 ⇒ PC ← PC+ΔPC |
| Cycles | 6–7 (see below) |
Bits marked ‘X’ in the instruction format above are don't-care values. The 9-bit literal is ignored for this instruction. This instruction needs an extra clock cycle when the skip is taken.
The SZ instruction tests register A. If the register is zero (depending on the MM used), the next instruction is skipped. Skipping is performed by adding ΔPC to PC, hence are skipped along the current direction of the PC.
Masking modes: masking modes apply to the comparison. Vector and scalar mode yield identical effects, testing the entire word. X and Y mode only test the rd and wo's bits respectively.
8.5.4. SNZ — Skip Unless Zero
| Instruction | SNZ A |
|---|---|
| Format | 0mm 100 XXX XXX aaa XXX |
| Semantics | X ≠ 0 ⇒ PC ← PC+ΔPC |
| Cycles | 6–7 (see below) |
This instruction is almost identical to SZ above.
Bits marked ‘X’ in the instruction format above are don't-care values. The 9-bit literal is ignored for this instruction. This instruction needs an extra clock cycle when the skip is taken.
The SNZ instruction tests register A. If the register is non-zero (depending on the MM used), the next instruction is skipped. Skipping is performed by adding ΔPC to PC, hence instructions are skipped along the current direction of the PC.
Masking modes: masking modes apply to the comparison. Vector and scalar mode yield identical effects, testing the entire word. X and Y mode only test the rd and wo's bits respectively.
8.5.5. DZ — Divert If Zero
| Instruction | DZ A |
|---|---|
| Format | 0mm 101 XXX XXX aaa XXX |
| Semantics | ΔPC ← (-1,-1); X = 0 ⇒ ΔPC←(1,1) |
| Cycles | 8–9 (see below) |
Bits marked ‘X’ in the instruction format above are don't-care values. The 9-bit literal is ignored for this instruction. This instruction needs an extra clock cycle if the register is zero.
The DZ instruction tests register A. If the register is zero (depending on the MM used), the PC moves southwest (ΔPC=(1, 1)). Otherwise, the PC moves northeast (ΔPC=(-1, -1)).
The ΔPC register is updated immediately. The next instruction to be fetched will be at address PC + ΔPC.
Masking modes: masking modes apply to the diversion (ΔPC assignment). Vector and scalar modes are identical, assigning southwest/northeast directions to ΔPC. X mode will assign west/east directions; Y mode will assign south/north directions. The following table illustrates this.
DZ A | DZ A.x | DZ A.y | |
|---|---|---|---|
| A = 0 | (-1, -1) | (-1, 0) | (0, -1) |
| A ≠ 0 | (1, 1) | (1, 0) | (0, 1) |
8.5.6. DNZ — Divert Unless Zero
| Instruction | DNZ A |
|---|---|
| Format | 0mm 110 XXX XXX aaa XXX |
| Semantics | ΔPC ← (-1, -1); X = 0 ⇒ ΔPC ← (1,1) |
| Cycles | 8–9 (see below) |
Bits marked ‘X’ in the instruction format above are don't-care values. The 9-bit literal is ignored for this instruction. This instruction needs an extra clock cycle if the register is non-zero.
The DNZ instruction tests register A. If the register is non-zero (depending on the MM used), the PC moves southwest (ΔPC = (1, 1)). Otherwise, the PC moves northeast (ΔPC = (-1, -1)).
Masking modes: masking modes apply to the diversion (ΔPC assignment). Vector and scalar modes are identical, assigning southwest/northeast directions to ΔPC. X mode will assign west/east directions; Y mode will assign south/north directions. The following table illustrates this.
DNZ A | DNZ A.x | DNZ A.y | |
|---|---|---|---|
| A = 0 | (1, 1) | (1, 0) | (0, 1) |
| A ≠ 0 | (-1, -1) | (-1, 0) | (0, -1) |
9. Epilogue: Whatever Happened to it?
What, you may ask, happened to the Fungs project? A lot, but very little was worth publishing. It did, however, ferment into an even more interesting project.
9.1. Assembler
After making the instruction set and writing the original draft paper, I wrote an assembler in Perl.18 It could parse code in columns separated by !, so it had its own weird, unique idiom. Here's an example.
; Another test: generates that classic ASCII cascade pattern that
; printers still use as their self-test.
.org 555,0
GOS
LV.x E,conchr.x
LV.y E,conchr.y
begin: LI A,#33
LI C,#15
GOS ! GOW
INC A,A ! l0: NOP
LI B,#79
DEC C,C
l2: OR D,A,0
DEC B,B ! TRP 64
SW D,E+0 ! JMP.y l0.y
INC D,D ! SZ C
SZ B ! SW D,E+0
JMP.y l2.y ! LI D,#10
GOE ! GON
The example starts at co-ordinates (555,0) in octal, or address 000555 (octal again, of course). The GOx single-instruction macros set the ΔPC to execute in the appropriate cardinal direction. The JMP macro simply sets the PC. Register E holds the conchr address. Writing to it causes a character to be printed on the console. The code loops around, printing rows of characters (starting with ASCII 33, !) and emitting a newline code every 79 characters printed. At the start of every line, the starting characters is incremented. 15 lines of this are printed, and then TRP 64 is called, which (I believe) was meant to halt the clock. Please note that, on the second column, the flow of execution is upwards (GOE at the bottom of the left column, followed by GON at the bottom of the right column).
9.2. VHDL Implementation
As I update this page, I had completely forgotten about this: there was a VHDL implementation of the Fungus CPU, most likely partial, almost certainly unsynthesiseable. This is quite interesting, since the original design purposefully left out such niceties as interrupts. The last code in the VHDL subdirectory hails from 2010, a good nine years after the first revision of the paper.
9.3. The Emulator
I originally had a Fungus emulator in Perl to test out simple programs. Eventually, I started building one in C using SDL as the display layer. I strapped on an emulated TMS9918 Video Display Processor and used the lot to make a fake, joke 80s micro (the Growth-83 by Fungal Computers Inc., obviously referred to as the ‘Fungal Growth’) using Fungus as the CPU. The ROM only ever contained code to decompress a soft font, stick it in the VDP's video RAM, turn on the display and print out a banner:
There's a cream for that.
The emulator's current, official state is limbo: it was made for a now ancient version of SDL, and won't even compile.
Historical and/or Inane Note
At one point, I decided to make Growth-83 an April Fools joke on The Machine Room, but I never got the time. That point was early in the machine's design, since both the fake model name and choice of the TMS9918 was purposeful. (it was an ubiquitous graphics chip in the early Eighties.)9.4. You Won't Believe What Happened Next!
(Sorry, I couldn't resist)
Writing my first Turing-complete architecture from scratch gave me a taste for more. I decided to get a physical Fungus machine running. (with numerous improvements, like a two-dimensional memory management unit, hardware contexts, etc.) As the design started growing a bit complex, I decided to implement a simpler one first as a feasibility test and started making notes on a 16-bit architecture of a more conventional ilk. That project took on a life of its own and became the CFT Project.
